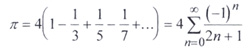TRANSMUTAÇÕES DO INFINITO O infinito atormentou, desde sempre, a sensibilidade dos homens; mais do qualquer
INTRODUÇÃO A transmutação do infinito adquire várias formas, de acordo com os diferentes pontos de vista considerados - o filosófico, o teológico, o físico ou o matemático. Serão aqui tratadas essencialmente as formas matemáticas, embora se faça referência a outros tipos de transmutação. O tratamento matemático do infinito será abordado com recurso a um mínimo de fórmulas ou de equações. Como diz Guillen em “Pontes para o infinito”1, uma confusão acerca da matemática consiste na suposição de que ela só pode ser convenientemente expressa em termos de símbolos. Para apoiar esta afirmação, Guillen cita um episódio da vida de Riemann (1826-1866), um dos mais importantes matemáticos do séc. XIX. Quando da sua admissão como académico na agora famosa Universidade de Gotingen, Riemann apresentou um trabalho sobre um tópico altamente técnico – os fundamentos da geometria – sem nele incluir uma única equação. Ora o infinito matemático é precisamente uma daquelas questões em que as ideias e a imaginação são o mais importante, tal como é patente na obra de Cantor (1845-1918), o matemático que mais contribuiu para esclarecer a questão do infinito. Para abordar a questão do infinito matemático será usada uma cronologia histórica. Começaremos com o período Grego, essencial no surgir do infinito matemático e filosófico. Também será referida a Idade Média, embora o que estivesse em causa, durante esse período, não fossem propriamente as questões matemáticas. No entanto, as especulações medievais são consideradas extremamente estimulantes no desenvolvimento matemático do período que se segue, o Renascimento. Foi durante esse período que nasceu o Cálculo Infinitesimal, principal instrumento matemático do tratamento do infinito. Serão apresentados, de forma sumária, alguns dos resultados e das técnicas obtidos pelos matemáticos dessa época. Finalmente far-se-á referência a algumas questões do infinito matemático na actualidade e também a abordagens não matemáticas do infinito. OS GREGOS E O INFINITO Os historiadores da matemática costumam referir o horror dos Gregos ao infinito. Seria interessante conhecer profundamente as causas de tal sentimento, que parece contradizer a sua capacidade matemática, até mesmo para tratar... o infinito. De facto os Gregos são, na matemática, os primeiros a tomar consciência da questão e, apesar de terem negado o infinito, deram-lhe um tratamento que deixou sementes. O infinito aparece pela primeira vez na história do pensamento quando os filósofos gregos tentam exprimir por um número a medida da diagonal do quadrado de lado 1. À representação geométrica finita corresponde um número que não acaba, um número infinito. “Poderemos, em consequência, dizer que o problema da diagonal do quadrado nos traz o infinito para ao pé da porta”2. Temos então uma transmutação de um segmento finito num número infinito . Os matemáticos gregos sabiam bem demonstrar, usando diversas técnicas, que esse número não podia ser expresso de forma finita3. Se tal fosse possível, haveria uma fracção ou, como se diz, um número racional, igual a v2 (raiz quadrada de 2). Os Gregos demonstraram também que essa fracção não existe4. Esses números que se exprimem por um número infinito de algarismos - que actualmente chamamos números irracionais - não existiam na matemática grega. Para os Gregos era impensável essa transmutação – o ter que usar um número infinito de algarismos para exprimir um segmento de recta tão bem definido como a diagonal de um quadrado. A medida de tal segmento exprimimo-lo hoje de forma finita usando o símbolo v2. Foi também uma transmutação, desta vez do infinito em finito, permitida pela álgebra, que encontrou símbolos para traduzir uma parte dos números infinitos. Existem muitos outros exemplos de segmentos de linhas rectas e curvas cuja medida escapava às possibilidades da matemática grega. Tais segmentos eram chamados incomensuráveis e a sua medida era considerada uma “grandeza” e não um número. Entre mais célebres encontra-se a circunferência de diâmetro 1 cujo perímetro vale pi, na notação actual. Aqui usamos uma letra para exprimir esta grandeza, também ela contendo um número infinito de algarismos. Já não é possível usar o símbolo “raiz” para definir a medida da circunferência de forma finita. O número pi é irracional mas de natureza diferente do atrás referido v2. Como se diz na matemática actual, é um irracional transcendente. Para tratar estes números e em particular a medida do perímetro da circunferência, foram utilizadas várias técnicas de transmutação do infinito em finito que iremos referir mais adiante. Embora os Gregos não considerassem os incomensuráveis como números, tentaram dar-lhes um estatuto de existência que equivale, de facto, a admiti-los como números. A teoria das proporções de Eudoxo foi o instrumento que permitiu definir os irracionais, recorrendo ao finito. A exposição dessa teoria, que figura no livro V dos Elementos de Euclides, sai do âmbito desta comunicação5, mas a sua ideia básica pode ser facilmente compreendida com auxílio do sistema decimal actualmente usado para escrever um número. Por exemplo, para definir o perímetro da circunferência de diâmetro 1 que sabemos medir pi, podemos dizer que esse valor é menor que 3,15 e maior que 3,14, ou seja, podemos escrever uma dupla desigualdade
Dizemos que esta aproximação é melhor que a anterior. Sendo pi um número que contém um número infinito de algarismos, fica definido de forma finita à custa desta “artimanha”. Este processo é a base do método da exaustão (descrito mais adiante) que permitirá aos Gregos resolver problemas do cálculo de áreas e volumes, problemas que serão retomados mais tarde pelos matemáticos renascentistas. O método da exaustão, embora servisse perfeitamente as necessidades de ordem prática, pois permitia encontrar valores aproximados das grandezas incomensuráveis, deixava em aberto o problema da natureza dessas mesmas grandezas. Esse problema só foi completamente resolvido no século XIX. Os incomensuráveis não são as únicas marcas de infinito na Grécia Antiga. O infinito surge na filosofia grega também de outra forma – através do problema da divisibilidade do espaço e do tempo. Esta questão, expressa através dos paradoxos de Zenão, divide atomistas e continuistas. Dois paradoxos ilustram a impossibilidade da existência de uma matéria divisível até ao infinito – os paradoxos de Aquiles e o da dicotomia. A impossibilidade do movimento se o espaço e o tempo serem compostos de partes indivisíveis é posta em evidência no paradoxo da flecha. Em qualquer dos casos, seja na hipótese continuista, seja na hipótese atomista, chega-se a um impasse. Esses paradoxos são conhecidos através dos textos de Aristóteles, que os enuncia antes de os criticar. Mas a crítica de Aristóteles recorre a argumentos do senso comum, não é uma crítica do ponto de vista da matemática. No entanto o pensamento de Aristóteles alimentou as especulações medievais acerca do contínuo e do infinito. Ele distinguia duas espécies de infinito - o actual e o potencial e negava a existência do primeiro. O infinito potencial, para Aristóteles, não apresenta nenhuma realidade física, é apenas uma construção do espírito necessário à resolução de certos problemas. O infinito potencial era admitido apenas no caso de grandezas contínuas infinitamente pequenas e de números infinitamente grandes. O tratamento que Aristóteles fez do problema foi qualitativo e metafísico. Mas, de facto, só usando instrumentos matemáticos - as séries e o cálculo infinitesimal - seria possível analisá-lo. Esses instrumentos permitiram não só resolver os paradoxos de Zenão como traduzir os números irracionais de forma finita, usando símbolos. Podemos dizer que são os mais eficazes instrumentos matemáticos de transmutação do infinito em finito. Eles integram uma extensa área da matemática chamada actualmente Análise Infinitesimal que será referida mais adiante. ARQUIMEDES E O MÉTODO DA EXAUSTÃO Na Quadratura da parábola, Arquimedes calcula a área do segmento parabólico. Ele inscreve sucessivos triângulos no segmento de parábola, calcula a área desses triângulos e vai obtendo valores cada vez mais próximos do pretendido, somando as áreas dos sucessivos triângulos. Assim demonstra que a área do segmento de parábola é igual a 4/3 da área do triângulo com a mesma base e com a mesma altura do segmento. No entanto Arquimedes não prolonga as somas até ao infinito. Ele deduz o seu valor demonstrando que não pode ser nem maior, nem menor que esses 4/3. Para calcular a área do círculo, Arquimedes considera polígonos inscritos de número de lados 6, 12,...96. Faz o mesmo com polígonos circunscritos e consegue assim mostrar que a área do círculo está entre dois valores determinados, ou seja, é menor que a dos polígonos circunscritos e maior que a dos polígonos inscritos. O resultado de Arquimedes, descrito na matemática actual equivale a considerar que
Apesar da grande originalidade dos trabalhos de Arquimedes, ele não teve discípulos directos na Grécia. Mas os matemáticos árabes interessaram-se pelo método da exaustão desde o séc. IX. Os irmãos Bana Musa usam-no pela primeira vez na literatura islâmica. O seu discipulo Thabit ibn Qurra (836-901) traduz “A esfera e o cilindro” de Arquimedes e na sua obra “Livro sobre a medida da secção cónica” mostra dominar perfeitamente o método. ESPECULAÇÕES MEDIEVAIS SOBRE O CONTÍNUO E O INFINITO Problemas como o infinito, o infinitesimal, a continuidade, eram o centro das discussões dos filósofos escolásticos. Estas questões eram estudadas à luz da filosofia peripatética e não em termos de pensamento matemático, mas as especulações que desenvolveram alimentaram o interesse por concepções que, mais tarde, se tornaram parte integrante da matemática.. Na matemática árabe, Ibn Qurra manipula o infinito como se tratasse de um outro número. Ele aceita que há infinitos maiores que outros, comparando, por exemplo o número de pares com o de inteiros. Já no Ocidente, durante a Idade Média, a questão do infinito era debatida no plano teológico. O infinito é tido como um atributo de Deus e representa a distância que separa o divino do humano. Mas tal como para os números infinitos, também para Deus havia representações finitas, as imagens. Estas podem ser consideradas como transmutações do infinito. As discussões medievais em torno do contínuo, dos indivisíveis e do infinito, desenvolviam-se a partir da teoria atomista. Um dos melhores exemplos do pensamento escolástico sobre estas questões é o de Thomas Bradwardine (1290-1349). Em Geometria especulativa e no Tratado do contínuo Bradwardine discute a natureza do contínuo, opondo-se a todas as formas de atomismo e afirmando que as grandezas contínuas são compostas por um número infinito de contínuos do mesmo tipo. O infinitesimal tinha, para este filósofo, tal como para Aristóteles, apenas existência potencial. Richard Swisneshead (~1350),mais vulgarmente conhecido por Calculator, estuda a natureza do infinito e as suas considerações têm alguma pertinência do ponto de vista matemático. Ele considera que não é possível estabelecer uma razão entre quantidades finitas e infinitas nem transpôr, para o tratamento do infinito, argumentos válidos para quantidades finitas. Cerca de duzentos anos mais tarde Galileu (1584-1642) vê mais claramente a diferença essencial entre as regras utilizadas no tratamento do finito e do infinito, estabelecendo correspondência entre agregados infinitos, em vez de razões entre quantidades finitas e infinitas - uma mudança que conduz à formulação final do cálculo, no séc. XIX. Do ponto de vista da matemática, enquanto que a aritmética e a álgebra despertaram interesse de alguns medievais, já o mesmo não aconteceu com outras questões trabalhadas pelos árabes e anteriormente pelos gregos. Uma delas é precisamente o método da exaustão e a sua aplicação ao cálculo de áreas. O Ocidente medieval ignora quase totalmente esses trabalhos de Arquimedes, assim como os dos árabes no mesmo domínio que, pode dizer-se, marcam o nascimento do cálculo infinitesimal. No entanto, as especulações escolásticas sobre o infinito, o infinitamente pequeno e a natureza do contínuo, reavivam o interesse pelo problema do infinito e preparam a entrada em cena das considerações infinitesimais, no séc. XVII. É importante referir que, na Idade Média, as discussões sobre a incomensurabilidade não eram orientadas no sentido da construção de conceitos matemáticos. As especulações medievais centravam-se sobretudo na questão metafísica da existência dos indivisíveis, e processavam-se em torno da distinção aristotélica entre infinito actual e potencial, desencadeada pelos paradoxos de Zenão. Apesar disso, desempenharam um papel de certo relevo no eclodir das concepções infinitesimais. O INFINITO NO RENASCIMENTO Em 1586 o engenheiro flamengo Stevin (1546-1620) utiliza o método de Arquimedes para determinar os centros de gravidade de figuras planas. Mas enquanto que Arquimedes considerava sempre um número finito de termos, Stevin toma um número infinito, no sentido de Aristóteles, ou seja, o de infinito potencial. Kepler (1571-1630) utiliza também o método da exaustão, considerando somas infinitas que calcula à custa de métodos intuitivos. Muitos outros matemáticos do Renascimento calculam áreas e volumes utilizando processos semelhantes ao método da exaustão, decompondo as suas figuras em infinitesimais ou em indivisíveis, como também eram chamados. Entre os mais famosos encontram-se Cavalieri (1598-1647), Torricelli (1608-1647), Roberval (1602-1675) e Gregoire de Saint-Vincent (1584-1667) que deu ao método de Eudoxo o nome de “método da exaustão”. Para Cavalieri uma linha é um conjunto infinito de pontos, uma superfície um conjunto infinito de linhas e um volume um conjunto infinito de planos. No entanto, para calcular uma área, em vez de somar esse número infinito de linhas, ele compara a superfície com outra que tenha o mesmo número de linhas. Gregoire de Saint Vincent preenche exaustivamente uma linha curva, não de pontos mas de segmentos de recta e refere explicitamente a soma de um número infinito de grandezas. Estas considerações vão originar o cálculo integral, em que se decompõe uma figura num número infinito de elementos e se soma efectivamente esse número infinito. Durante o século XVII, a álgebra desenvolvida pelos árabes e pelos matemáticos do Renascimento assim como os cálculos com infinitesimais, geram uma confiança ilimitada nas possibilidades do simbolismo. Desaparecem os interditos relativos à manipulação do infinito, sobretudo após Newton (1642-1737) e Leibniz (1646-1716). Os cálculos feitos com polinómios, como por exemplo a fórmula do binómio de Newton, são generalizados às somas infinitas. Estes resultados são justificados “segundo o princípio de generalidade da álgebra”. As somas infinitas eram de facto calculadas o que permitiu resolver o paradoxo da dicotomia. O cálculo da soma dos segmentos (1/2+1/4+1/8+...) até ao infinito dava um resultado finito. Essa soma infinta, chamada série, é a melhor evidência de transmutação de infinito (número infinito de termos) em finito (valor finito). A manipulação de somas infinitas tornou-se de uso corrente na matemática. As séries tornam-se um instrumento de expressão finita dos números irracionais algébricos e transcendentes. De facto, o símbolo E (sigma) usado para representar uma soma, permite traduzir, de forma finita, números para os quais não havia qualquer representação, a não ser a representação geométrica ou uma letra, como por exemplo o número pi:
Apesar de todas as inovações introduzidas pelo cálculo infinitesimal, Leibniz só concebia o infinito ou o infinitesimal como quantidades auxiliares facilitando o cálculo, cujo resultado se exprimia sempre em termos de quantidades finitas. Um infinitésimo era uma quantidade que tão depressa era nula, quando comparada com uma grandeza finita, como era grande, quando comparada com um infinitésimo de ordem superior. O infinitamente grande era uma quantidade que nunca atingia o infinito. “O cálculo infinitesimal é útil quando se trata de aplicar a matemática à descrição dos fenómenos de física, no entanto não serve para definir a natureza das coisas”, afirmava Leibniz. É uma nova versão das posições de Aristóteles, apoiada agora pelas novas técnicas matemáticas. O Renascimento é uma época de explosão criativa, onde os problemas dos fundamentos são postos de lado e a preocupação dos gregos com o rigor é mesmo considerada excessiva. No entanto, apesar da enorme capacidade de manipulação do infinito, havia falhas na interpretação do formalismo utilizado. A natureza dos infinitesimais não estava definida e alguns autores, entre os quais Berkeley (1685-1753) não aceitavam a sua existência, apesar do cálculo conduzir a resultados certos. A imprecisão existente na interpretação do significado do cálculo infinitesimal provocou as críticas não só de Berkeley mas também de Nieuwentijt (1654-1718). “As críticas de Berkeley e Nieuwentijt tinham a sua justificação, mas eram inteiramente negativas. Eram incapazes de fornecer uma fundamentação rigorosa do cálculo, mas inspiraram trabalhos construtivos posteriores”7. A fundamentação rigorosa do cálculo só viria a ser elaborada dois séculos depois. Nos séculos XVIII e XIX os matemáticos, para além de desenvolverem os métodos do cálculo infinitesimal, vão tentar fundamentar rigorosamente esses métodos. Sai fora do âmbito deste trabalho a explicação dos resultados obtidos, nessa direcção, por Euler (1707-1783), d’Alembert (1717-1783), Lagrange (1736-1813) e muitos outros matemáticos. Os esforços de todos eles conduziram a uma formalização rigorosa do cálculo baseada no conceito de limite e que foi elaborada durante o século XIX por Cauchy (1789-1857), Bolzano (1781-1845) e Weierstrass (1815-1897). O conceito de limite permitiu dar ao infinito um novo tratamento matemático. UMA DEFINIÇÃO DE INFINITO MATEMÁTICO A história matemática do infinito atinge o seu verdadeiro apogeu com Cantor. Como diz Bertrand Russel8(1872-1970), “embora muita gente, desde os Gregos, tenha falado do infinito com grande à vontade, nunca ninguém pensou em perguntar, o que é o infinito?”. Mas “Dedekind e Cantor formularam esta questão e, o que é mais extraordinário, deram a resposta. Eles encontraram, por assim dizer, uma definição precisa de um número infinito ou de uma colecção infinita de objectos”. Os primeiros estudos sistemáticos de conjuntos infinitos são devidos a Dedekind (1831-1916) e a Cantor. Dedekind estabelece uma bijecção entre dois conjuntos infinitos, uma noção capital para a teoria dos conjuntos. Essa bijecção equivale a dizer que determinados conjuntos infinitos têm o mesmo número de elementos. Por exemplo existem tantos números pares como inteiros positivos. Esta maneira de definir um conjunto infinito como um conjunto em bijecção com uma das suas partes é interessante sob dois pontos de vista: para já não se trata agora de um infinito potencial mas sim do próprio infinito, tratado na sua totalidade. Estamos em presença do infinito actual e não do infinito potencial. Por outro lado o infinito não é mais a negação do finito. Pelo contrário, o finito é que é a negação do infinito. Um conjunto finito é aquele que não está em bijecção com nenhuma das suas partes. Podemos resumir estas ideias dizendo que face aos paradoxos do infinito, negando um dos pilares da matemática grega (o todo é maior que as partes), os matemáticos, seguindo Dedekind, resolveram agarrar no problema ao contrário. Existem todos tão grandes como algumas das suas partes. Definamos então um conjunto infinito como aquele que é tão grande como algumas das suas partes. Isto é apenas uma habilidade genial ou antes um acto fundador de uma matemática pertinente? As contribuições de Cantor para a teoria dos conjuntos são ainda mais originais que as de Dedekind. A obstinação de Cantor relativamente ao infinito leva-o a formular conceitos que irão revolucionar o pensamento matemático. Um desses conceitos foi o de transfinito. “Existe, depois do finito, um transfinito, ou seja, uma escala ilimitada de modos determinados, que por natureza são infinitos, e que no entanto podem ser definidos de maneira precisa, tal como o finito, por números determinados, bem definidos e distintos uns dos outros.” Para caracterizar o “tamanho” de um conjunto infinito, Cantor introduz a noção de equipotência entre conjuntos infinitos. Dois conjuntos infinitos têm o mesmo tamanho, se são equipotentes ou têm o mesmo Cardinal. Os números naturais têm Cardinal Sabemos que os subconjuntos infinitos de N têm o mesmo cardinal, pois existe uma bijecção entre esses conjuntos, ou seja,
Ao possuir um símbolo próprio para representar o infinito, estamos a criar uma aritmética que situa para além dos números finitos, uma aritmética transfinita. Segundo Cantor, os inteiros, qualquer subconjunto dos inteiros ou naturais têm a potência dos naturais. Em 1874 Cantor provou que também os irracionais algébricos têm o mesmo cardinal dos naturais. Pelo contrário, os reais e, em consequência, os irracionais e os transcendentes não são equipotentes a N.. Diz-se que R (conjunto dos números reais) tem a potência do contínuo. O seu Cardinal é c. Um conjunto com a mesma cardinalidade de N.. diz-se que é numerável, ou que tem a potência do contínuo. Sabemos que também Z é numerável, mas que já R é tal que
Os trabalhos de Cantor reacenderam a polémica sobre o infinito no seio da comunidade matemática. Um dos promotores do debate foi Kronecker, que tentou impedir a publicação dos primeiros artigos de Cantor, onde ele demonstrava que o conjunto dos reais não é numerável e que o conjunto dos pontos de um quadrado é equivalente ao conjunto de pontos do seu lado. Mas Cantor foi apoiado por Dedekind e, mais tarde, por Hilbert. Outros matemáticos, para além de Kronecker, recusam o infinito actual e aceitam apenas o potencial. Eles são Henri Poincaré, Brouwer e Hermann Weil. Estes dois últimos consideram que apenas os números inteiros são objecto de uma intuição indiscutível, dados como sucessão não limitada e não como conjunto bem definido. A demonstração da indecidibilidade pôs fim às controvérsias, permitindo a legitimidade de opções contraditórias. Cantor, por seu lado, não reconhecia a existência dos infinitamente pequenos e foi preciso esperar pela Análise não standard, formulada por Robinson (1918-1974) em 1966, para os ver reconhecidos como entidades bem definidas e assim justificar os cálculos que os físicos faziam com os infinitésimos. Pode dizer-se que a análise non-standard representa a aritmetização do infinitamente pequeno, tal como a teoria de Cantor representa a aritmetização do infinitamente grande. Tanto uma como outra foi usada na prática muito antes de possuírem um estatuto de rigor. Com a análise non-standard mais uma vez o infinito origina inovação. Joseph Dauben9 refere-se-lhe como causa de revolução contemporânea na matemática, semelhante a outras revoluções que, no passado, transformaram profundamente a natureza da disciplina. Muitos autores consideram que na matemática não tem sentido considerar o conceito de revolução10, enquanto que para outros há exemplos que demonstram o contrário. Seja qual for a posição que se tome, não há dúvida que a questão do infinito originou controvérsia e reviravolta, mesmo depois dos matemáticos terem aprendido a manipulá--lo com os instrumentos criados pelo cálculo infinitesimal. O infinito, surgido na ciência e filosofia gregas, foi trabalhado do ponto de vista matemático ao longo dos séculos, o que originou grandes inovações. Mas esse tratamento não esgotou a questão que tem outras formas de abordagem às quais serão feitas breves referências. O INFINITO FÍSICO Arquimedes é talvez o primeiro a dar ao infinito o sentido que ele tem para os físicos. Tentando combater o pensamento de Aristóteles e a sua negação do infinito actual, Arquimedes considera que é possível escrever um número maior que o número de grãos de areia necessários para encher o Universo. Ele estima esse número em 1051, um número infinito. Aquilo que Arquimedes fez, e que é falso do ponto de vista matemático, é o que os físicos fazem todos os dias na sua actividade diária. De facto, os físicos consideram que certos valores são infinitos, quando comparados com outros. Assim, a velocidade da luz é tida como infinita em certos cálculos, assim como a massa da terra ou a do sol. Tudo se resume a comparar ordem de grandezas sendo essa verdade física apenas operativa, ou seja, limita-se a ser usada num contexto bem determinado, sem consequência sobre a natureza dos objectos. Nessa perspectiva, pode dizer-se que, na física, o infinito é apenas algo muito grande, ou muito rápido, ou muito pesado. Nesse sentido o infinito físico tem pouco a ver com o infinito matemático apesar dessa comparação de ordens de grandeza ser de natureza matemática. Uma questão que pode ter alguma pertinência, no que diz respeito à relação entre o infinito matemático e o infinito físico é levantada por Hans Hahn11, ao tratar o problema do espaço. “O espaço do nosso mundo físico tem extensão finita ou infinita?”, ou seja, qual dos modelos de espaço é mais adequado para descrever a realidade, já que na matemática se podem considerar os dois - o modelo do espaço infinito da geometria euclidiana ou o espaço finito da geometria Riemaniana? A mesma questão se poderia colocar para o tempo ou para a matéria. De certo modo, podemos dizer que na física actual essas questões não têm sentido. A correspondência entre os objectos matemáticos e a realidade física não pode ser debatida a priori, antes de saber como é que eles vão ser utilizados para descrever a realidade. A matemática apenas fornece modelos de comportamento e não é de forma alguma contraditório considerar que o espaço é finito, em certas descrições, enquanto que noutras é tomado como infinito. Os objectos matemáticos e também o infinito matemático são construídos independentemente da realidade material, mesmo que, frequentemente, pareçam traduzir essa realidade. O facto de, na matemática, existir uma noção aperfeiçoada de infinito não implica, necessariamente, que isso corresponda a algo de existente. Considerar que assim é seria transpor para as relações entre a física e matemática o argumento de Descartes que apresentava como prova da existência de Deus o facto de existir em nós a ideia de infinito. A ideia de infinito em outras áreas do pensamento surge, tal como na física, associado ao muito grande, ao muito longo, ou ao muito intenso. Quando se trata de descrever sentimentos, razões ou saberes “infinitos” é adequado usar exactamente os mesmos termos que na física. Quando dizemos que dois sentimentos de dor ou prazer são incomparáveis, estamos a falar de diferentes ordens de grandeza, o que significa que um deles pode ser tomado como infinito em relação ao outro. As ideias e a linguagem da física são mais adequadas do que a da matemática para descrever os infinitos acessíveis ao senso comum. De facto, a compreensão do infinito matemático obriga a conhecimentos técnicos, apesar de ter como ponto de partida ideias simples. Tanto a formulação da ideia da continuidade do espaço, como a aritmética transfinita e a análise non-standard são matérias dificilmente acessíveis a um não matemático. Estudar o infinito matemático implica adquirir conhecimentos extensos e profundos sobre variadíssimos temas que por vezes parecem estar bem longe do aliciante tema inicial - o infinito. 1 Guillen, M., "Pontes para o Infinito", Gradiva, Lisboa, 1998, p. 14.
|