
|
|
JOSÉ CASQUILHO::::......:::: |
 |
|
Dos números: entre signo e valor |
|
 |
|
(…) en employant au lieu des nombres eux-mêmes, des signes ou symboles
généraux qui n’aient aucune relation particulière avec les valeurs des
nombres qu’ils représentent. Pour attendre ce but on fait usage des
lettres de l’alphabet.
E. Tarnier [1]
Number
signs probably preceded number words, for it is
easier to cut notches in a stick than it is to establish a
well-modulated phrase to identify a number.
Carl B. Boyer [2] |
|
 |
|
A
meu ver poucas histórias há tão belas como as dos números, conceitos ou
entes mentais que se foram construindo num processo gerativo onde
concorreram várias culturas, ao longo de milénios, erguendo uma
linguagem universal da humanidade.
Do
lado do pensamento ocidental já Aristóteles tinha esclarecido que número
é número de alguma coisa, um índice específico, enquanto que Platão em A
República antecipava [3] que o cálculo e a aritmética versam
inteiramente sobre o número e eram ciências próprias para conduzir à
verdade.
A
propósito da unidade e recordando Euclides: o um é aquilo em virtude do
qual cada um dos seres é dito uno, e os números são a multiplicidade
constituída de unidades [4]. Falamos aqui dos números naturais, inteiros
positivos, herdados do problema da contagem, a que outros na
Antiguidade, salientando-se Diofanto [5], o autor de
Arithmetica, acrescentaram os números gerados pelos problemas da
medida, sobretudo relacionados com comprimentos e áreas, que envolviam o
cálculo de frações e raízes na solução de equações. É sabido [6] que os
matemáticos gregos, tendo a noção de grandeza incomensurável, mas não
tendo a noção correspondente de número irracional, constituíram a
matemática sob forma geométrica, considerando em vez de números
segmentos de recta, para assim abrangerem as grandezas comensuráveis, os
números racionais, e as incomensuráveis.
Na
citação em epígrafe de Tarnier vê-se que na álgebra, no final do século
XIX, se colocava no lugar dos números propriamente ditos signos
ou símbolos gerais que têm uma relação arbitrária com os
valores dos números que representam - e assim
são substituídos por letras do alfabeto.
O
signo, semeion em grego, era para os estóicos uma entidade
que significava mediante um incorporal, uma implicação [7], não
redutível a qualquer expressão física que lhe estivesse associada; os
incorporais não são coisas, são estados de coisas, modos de ser; o
lekton, o dizível, é dessa categoria e no seu sentido pleno
é uma proposição. Os estóicos quando falam de signo referem-se a algo de
imediatamente evidente que se reporta a outro algo não imediatamente
evidente.
O
signo como aliquid stat pro aliquo - algo que está no lugar
de alguma outra coisa -, era a definição clássica herdada que Peirce em
1897 refinou como sendo [8]: algo que está para alguém por algo sob
algum aspecto ou capacidade.
As
letras do alfabeto são símbolos, definindo-se símbolo como um signo
vagamente codificado. Pode-se ver que a utilização diacrónica de letras
do alfabeto em matemática vai ficando cada vez mais imersa num campo que
lhes adensa o significado: semântico, portanto.
Também se pode apelar a uma redução binária: desde Saussure que o signo
pode considerar-se um valor [9] representado num significante físico, a
que se associa um significado mental, e ainda ser considerado nos eixos
da sincronia e da diacronia; a linguagem seria assim o processo
semiológico por excelência onde a semântica é referida como tendo por
objecto analisar deslocamentos da relação entre o significado e o
significante.
O
valor de um número pode assim ler-se como o número
propriamente dito inserido num sistema ordenado e expresso num código,
por exemplo escrito em linguagem decimal - o conjunto
{0,1,2,3,4,5,6,7,8,9} foi adquirido como alfabeto numérico na Europa
desde que Leonardo de Pisa, em 1202, escreveu o
Liber Abaci com que introduziu na Europa o sistema de numeração
hindu-árabe incluindo um pequeno círculo para símbolo do zero [10, 11]. |
|
 |
|
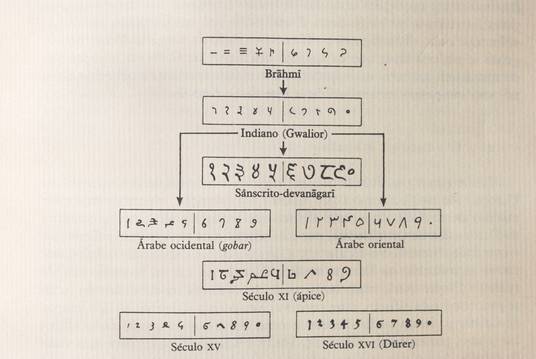
Árvore
genealógica do sistema de numeração hindu-árabe |
|
Ainda hoje os primeiros dígitos do sistema decimal não têm a mesma
probabilidade de ocorrência nos números encontrados na vida real [12],
aparecendo o número 1 com maior frequência, cerca de 30 por cento,
enquanto o número 9 apenas ocorre na ordem de 4 por cento.
As
letras do alfabeto começam por ser incógnitas na resolução
de equações, tomando o lugar de coisa, verificando as
ligações sintáticas das fórmulas que as operações envolvidas tornam
possíveis, das quais se extraem soluções, incluindo a solução ‘não ter
solução’: o conjunto vazio de soluções, representante de uma
impossibilidade no campo dos números admissíveis no contexto ou quadro
axiomático em que o problema se admite bem colocado.
Em
termos actuais diz-se que [13]: nas aplicações das matemáticas um número
real Y é quase sempre substituído por um número racional X, que é um
valor aproximado deste; quer dizer que a diferença Y-X está compreendida
entre –ε e + ε, em que ε é um número positivo a que se chama a
aproximação de Y por X, ou o erro cometido sobre Y; X é chamado um valor
aproximado de Y a menos de ε, sendo o próprio Y considerado como o seu
valor exacto.
Essas letras do alfabeto, latino, grego ou ainda outros como o hebreu,
constituem a designação de (números) variáveis na teoria
das funções: aplicações que transformam um objecto do domínio numa
imagem que se expressa no contradomínio. Essas variáveis podem vir a
constituir variedades [14, 15], estruturas matemáticas
elaboradas que podem ser reais ou complexas. A variedade dos equilíbrios
de um sistema dinâmico é um exemplo e a variedade de informação segundo
uma dada métrica é outro.
Como nos reporta Caraça [16] foi a superação sucessiva de
impossibilidades numéricas pelo engenho humano, e a sua internalização
no sistema, que permitiu alargar mais e mais o conceito de número; do
número natural passou-se aos racionais através do cálculo de frações,
depois aos irracionais através de raízes e ainda outras excursões que
atingem os infinitos de Cantor.
A
essa conquista pela extensão sucessiva dos números reais resistiu a
unidade imaginária, a raiz quadrada de menos um, impossível de
internalizar por razões de incompatibilidade lógica com o sistema dos
números reais a partir do argumento de que não há áreas negativas, mas
ainda assim insidiando-se misteriosamente no cálculo de tal forma que é
atribuída a Hadamard a citação de que o caminho mais curto entre duas
verdades no domínio real atravessa o domínio complexo [17].
Na
geometria fractal existe o conceito de dimensão de informação [18], um
número real, que mede a variação de informação no comportamento dinamico
de um sistema caótico. A dinamica simbólica é usada para analisar a
dinamica de funções e uma função diz-se caótica se manifesta dependência
sensível das condições iniciais [19], podendo ser fortemente caótica se
além de ser caótica tiver um conjunto denso de pontos períodicos e
transitividade. Uma aplicação do espaço de fase para o espaço dos
símbolos é designada por dinâmica simbólica [20] e consequentemente o
caos pode ser visto como um gerador de símbolos se se provir um código
no espaço de fase [21]. No entanto, Mandelbrot recordava-nos que quando
a medida de complexidade de um conjunto é obtida pelo menor comprimento
do (melhor) algoritmo disponível num dado alfabeto se conclui que uma
curva fractal imbrincada é mais simples do que um círculo [22]; ou seja,
de acordo com essa métrica, o círculo, símbolo da mónada, é mais
complexo do que uma complicada linha requebrada.
Alguns reclamam que a informação é apenas física [23], definindo
informação quantica como a que é transportada por um sistema físico
obedecendo às leis da mecânica quantica. Mas outros observam que a
informação quantica, quando ocorre entrosamento, tem como consequência
que se observam eventos físicos cuja distribuição marginal não é
consistente com nenhuma distribuição conjunta e assim ofende-se o
princípio do realismo local [24].
Há
autores que esclarecem que adoptar a posição epistémica do realismo
científico não implica rejeitar entidades não físicas [25]. O conceito
de episteme organizado por Greimas e Courtés [26] define-se
como a organização hierárquica de vários sistemas semióticos capaz de
gerar, através de uma combinatória e regras de (in)compatibilidade, o
conjunto de manifestações cobertas por esses sistemas numa dada cultura.
Também Eco nos lembra que [27] a informação da mensagem não se confunde
com a informação na fonte, esta era informação física, computável
quantitativamente, e aquela é informação semiológica, não computável
quantitativamente, mas definível através da série de significados que
pode gerar, uma vez posta em contacto com os códigos. Recorde-se que o
código [28] é um sistema de signos que, por convenção e de acordo com
regras pré-fixadas, está destinado a representar e transmitir a
informação entre emissor e receptor.
O
par de informação física/semiológica é relevante da distinção
significante/significado e pode-se alegorizar através da Pedra da
Roseta: os hieroglifos egípcios estavam lá, marcados na pedra ou
pintados, significantes, mas não se conseguiam decifrar e interpretar
até ter um código que o viabilizasse.
Em
geral, retomando Umberto Eco pode dizer-se que entre o significado e o
símbolo incorrem relações onomasiológicas, conferindo determinados nomes
a significados, ao passo que entre o símbolo e o significado existem
relações semasiológicas, onde determinados símbolos designam
significados. Assim acontece com as letras em matemática, conforme o
contexto podem ser números constantes ou variáveis e na teoria de
funções representar objectos, imagens, e ainda parametros, que cobrem ou
resolvem-se em conjuntos de números. |
|
 |
|
Tableta YBC 7289, coleção da Yale University, dinastia de Hamurabi [29];
o autor refere que feitas as conversões adequadas está representado o
número 1,414213 que é a expansão decimal aproximada da raíz quadrada de
2. |
|
Falar de valor real em vez de número real e de
valor complexo em vez de número complexo é corrente, sendo que o
primeiro é um escalar, representado por um ponto numa recta com origem e
sentido de ordenação e o segundo é representado no plano cartesiano como
um vector. O valor real é um escalar e o valor complexo é um vector,
signo da força, expresso como z=x+iy ou (x,y) supondo a base (1,i),
próximo de uma denotação do par informacional físico/semiológica,
emparelhado com o par saussureano significante/significado, por sua vez
análogo do par valor de troca/valor de uso que se utiliza na economia.
O
universo dos números é fascinante. Para além dos números reais e fazendo
uso dos transfinitos de Cantor controem-se números surreais [30]; estes
últimos formam eventualmente a coleção de todos os números concebíveis
pelo engenho humano até hoje, mas não formam um conjunto: seria o
conjunto de todos os conjuntos que se demonstra conduzir a uma
contradição, violando a lei da cardinalidade. |
|
 |
|
Referências: |
|
[1] E. A. Tarnier. 1857. Éléments d’ Algèbre. Librairie de la Hachette
et Cie, Paris.
[2]
Carl B. Boyer. (1968) 1991.
A History of Mathematics. John Wiley & Sons, Inc., New York.
[3]
J. Guinsburg. 2006. A Republica de Platão. Editora Perspectiva SA, S.
Paulo, pag. 279
[4]
Ambrogio G. Manno. 1982. A Filosofia da Matemática. Edições 70, Lisboa,
pag. 26
[5]
http://pt.wikipedia.org/wiki/Diofanto_de_Alexandria
[6]
Francisco G. Teixeira. 1934. História das matemáticas em
Portugal.Arquimedes Livros, Lisboa, 2006.
[7]
Umberto Eco. 1994. Signo. Enciclopédia Einaudi, vol 31, Signo,
p:11-51, Imprensa Nacional Casa da Moeda, Lisboa
[8]
Umberto Eco. 1994. Significado. Enciclopédia Einaudi, vol 31,
Signo, p:52-97, Imprensa Nacional Casa da Moeda, Lisboa
[9]
Ferdinand de Saussure. 1916 (1971). Curso de Linguística Geral.
Publicações Dom Quixote Lda., Lisboa, 1999.
[10] Giulio Giorello e Marco Mondadori, 1989. Zero.
Enciclopédia Einaudi, vol.15: Cálculo-Probabilidade,
pp: 64-99.
[11]
http://br.monografias.com/trabalhos915/da-triade/da-triade.shtml
[12] Nuno Crato. 2008. A Matemática das Coisas. Gradiva, Lisboa.
[13] Jean Dieudonné. 1987. A Formação da Matemática Contemporânea (Pour
l’honneur de l’esprit humain – Les mathématiques aujourd’hui),
Publicações Dom Quixote Lda, Lisboa, 1990.
[14]
http://pt.wikipedia.org/wiki/Variedade
[15]
http://www.math.ist.utl.pt/~rfern/GD/notaspI.pdf
[16] Bento de Jesus Caraça. 1946. Conceitos Fundamentais da Matemática.
Livraria Sá da Costa Editora, Lisboa, 1984.
[17] cf. Paul J. Nahin. 2007. An Imaginary Tale. Princeton University
Press, New Jersey.
[18] Manfred Schroeder. 1991. Fractals, Chaos, Power Laws. W. H. Freeman
and Company, New York.
[19] Denny Gulick. 1992. Encounter with Caos. McGraw-Hill, Inc., New
York.
[20] Christian Beck e Friedrich Schlögl. 1993. Thermodynamics of chaotic
systems – an introduction. Cambridge University Press, Cambridge, 1995.
[21] Kunihico Kaneco e Ichiro Tsuda.
2001. Complex Systems: Chaos and Beyond. Springer-Verlag, Berlin.
[22] Benoit B. Mandelbrot. 1983. The Fractal Geometry of Nature. W. H.
Freeman and Company, New York.
[23] Dénes Petz. 2008. Quantum Information Theory and Quantum
Statistics. Springer- Verlag, Berlin.
[24] Thomas M. Cover e Joy A. Thomas. 2006. Elements of Information
Theory. John Wiley & Sons, Inc., Hoboken.
[25] Stathis Psillos. 2006.
Scientific Realism and Metaphysics. Metaphysics in Science (ed. A.
Drewery), Blackwell Publishing, Malden, pp: 14-32.
[26] cf. Jacques Fontanille e Claude Zilberberg. 1998. Tensão e
Significação. Discurso Editorial, São Paulo, 2001.
[27] cf.
http://www.triplov.com/casquilho/2009/Mensagem/index.html
[28] Miquel R. Alsina. (1989) 1995. Los Modelos de la Comunicación.
Editorial Tecnos, S.A., Madrid.
[29] Eli Maor. 2007. The Pythagorean Theorem. Princeton University
Press, Princeton.
[30]
http://pt.wikipedia.org/wiki/N%C3%BAmero_surreal |
|
 |
José Pinto Casquilho.
Centro de Ecologia Aplicada Baeta Neves
(CEABN/UTL), Centro de Estudos de Comunicação e
Linguagens
josecasquilho@gmail.com
(CECL/UNL).
|
|
|