Morfogénese: borboleta cauda de andorinha

Nas cáusticas de luz [2] vimos a cúspide associada à ruga, e foi dito que se lhe seguia a cauda de andorinha. Podemos recordar o contexto: estamos no âmbito da Teoria das Catástrofes e da elaboração da lista das sete catástrofes elementares, correspondentes ao desdobramento universal de um polinómio - entendido como função de Lyapounov [3] - que governa um sistema dinâmico que se expressa numa dinâmica; os pontos em que o gradiente se anula são os equilíbrios, podem ser estáveis ou instáveis, ou ainda degenerados, e estão reunidos numa variedade real. Estamos fora do âmbito das variedades complexas, aqui não intervêm números imaginários.

No plano real Peirce referiu as cúspides e inflexões como singularidades ordinárias bem como os pontos estacionários e as tangentes , e ainda definiu uma singularidade de tipo superior como sendo uma que difere muito pouco de um agregado de singularidades ordinárias. Peirce analisava as singularidades no plano cartesiano [4] mas é possível fazer uma extensão para o espaço com mais dimensões.

É assim que se vê que a ruga é formada por duas dobras, sendo a dobra a catástrofe elementar, e a cauda de andorinha é formada por uma ruga e uma dobra. O nome cauda de andorinha foi sugerido pelo matemático cego francês Bernard Morin [5].

Também vale a pena recordar que o termo catástrofe não tem aqui a conotação negativa da linguagem corrente, corresponde a uma transição abrupta, uma transição de fase, mas tanto pode ocorrer num sentido negativo como positivo. Nas palavras de Thom era essa transição abrupta, uma descontinuidade no comportamento, que muitas vezes salvava o sistema. Aliás Thom preferia designar o tema geral como morfogénese[6] retomando a expressão de Alan Turing, e insistia que a TC era uma linguagem e um método que visa encontrar o modelo dinâmico mais simples capaz de explicar uma morfologia empírica.

O conjunto catastrófico num tal sistema dinâmico é o complementar do conjunto aberto dos pontos regulares - é o conjunto fechado dos pontos singulares -, também chamado conjunto de bifurcação, entendendo-se por singularidade uma figura que se concentrou num ponto; o conjunto catastrófico obtém-se projectando a sub-variedade dos equilíbrios degenerados no espaço definido pelos parâmetros de controlo.

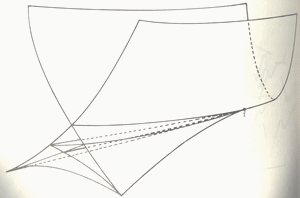
Tinha-se uma boa imagem na cúspide e também se tem uma boa idéia na figura seguinte onde o ponto f se designa ponto cauda de andorinha e à medida que nos aproximamos do ponto, fazendo um corte vertical, vê-se que a estrutura permanece a mesma, embora cada vez mais pequena: condensação progressiva da figura num ponto.

Fig. 1 - esquema do conjunto catastrófico cauda de andorinha
em que o ponto f é o ponto cauda de andorinha [7]

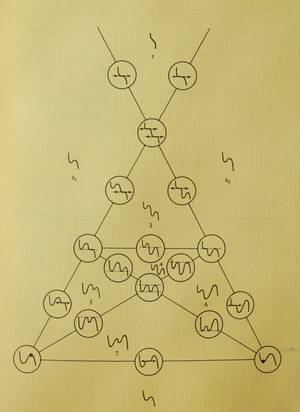
No diagrama seguinte apresenta-se a configuração dos diferentes equilíbrios do sistema (inflexões, mínimos e máximos) segundo um corte vertical nesse esquema.

Fig. 2 - corte vertical do esquema anterior mostrando a taxonomia
das funções estabilizadas [8]

A cauda de andorinha e a borboleta são as duas catástrofes elementares que fecham a sequência das que têm uma só variável de comportamento (ou de resposta) - designadas genericamente por cuspóides - e vários parâmetros. O ponto de partida é a não-catástrofre elementar: o mínimo de uma função potencial, o estado elementar do ser, que se coloca como hipótese e que funda a estabilidade estrutural.

Fig. 3 - caracterização das singularidades cauda de andorinha
e borboleta na lista de Thom[9]

O desdobramento universal da cauda de andorinha expressa-se canonicamente como uma fórmula com três parâmetros de controlo {u,v,w} e uma variável-resposta x inserida na arquitectura de um polinómio de grau 5. Usando a interpretação cinemática de Peirce na caracterização da cúspide[10], também na cauda de andorinha podemos ensaiar uma leitura cinemática sobre o diagrama canónico interpretado como um legissigno icónico remático[11] na classificação de Peirce, comportando uma lei.

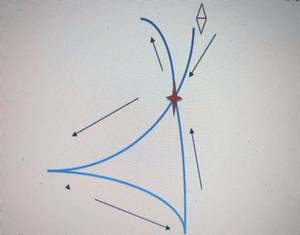
Fig. 4 – diagrama simplificado da cauda de andorinha com leitura cinemática

Nesta leitura o ponto f representa um ponto de retorno, trata-se no entanto de um regresso ao futuro, já que segue por uma linha diferente da trajectória original, onde à conta de duas cúspides (sendo uma delas dupla) regressou à direcção principal mas sentido diverso – a cauda de andorinha pode ser vista como a figura do retorno, a que podemos associar a parábola de que as andorinhas anunciam o regresso da Primavera. Petitot caracterizou-a como sendo a figura da deixis[12], um sistema de indicadores.

A cauda de andorinha foi o título e o tema do último quadro de Salvador Dali.

Fig. 5 - Salvador Dali, 1983: Swallowtail

Sucede que a cauda de andorinha tem poucos equilíbrios estáveis quando comparados com os instáveis, para um grande número de condições, pelo que não é um bom modelo qualitativo para fixar estados empíricos. A catástrofe que se lhe segue - a borboleta - pelo contrário, contém três camadas distintas de equilíbrios estáveis, representando a intermédia um compromisso entre as outras duas.

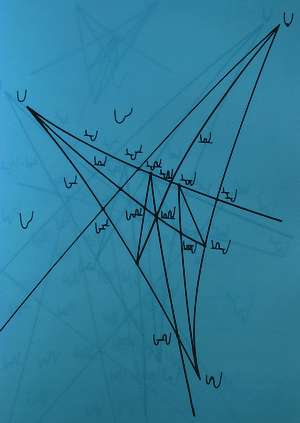Fig. 6 – secção do diagrama de fase da catástrofe borboleta[13]

Fig. 7 – borboleta cauda de andorinha, foto da Wikipedia

A catástrofe borboleta tem uma fórmula que comporta uma variável-resposta e quatro parâmetros. Que interpretação podemos fazer disto? Imaginemos, a propósito da situação contemporânea de crise internacional que a variável resposta representa um índice de confiança e então os quatro parâmetros que definem o espaço de controlo podem ser entendidos como índices de verdade, liberdade, igualdade e solidariedade: {v,l,i,s}. A confiança é função daqueles quatro parâmetros e a sua retoma exige uma concertação adequada. Na cauda de andorinha temos à mesma uma variável resposta e três parâmetros, seja {v,l,i}, é a falta de solidariedade que instabiliza a situação dir-se-ia; outras interpretações são possíveis, obviamente, a falta de aderência à verdade é letal para a credibilidade do sistema.

Estamos a falar de morfogénese, o tema que foi introduzido por Alan Turing[14] a partir da formulação matemática de processos de reacção-difusão, e que era o quadro a partir do qual Thom enunciava os modelos.. A palavra chave é desdobramento universal [15] de um polinómio definido como um desdobramento versal com o número mínimo de parâmetros, no âmbito da teoria da estabilidade estrutural.

Também em Ecologia o tema é recorrente, o espaço de Turing ficou uma referência conceptual [16], sendo aplicada a definição de catástrofe ao caso em que uma população decresce abruptamente de um estado de abundância para baixa densidade [17], rarefacção,  podendo ser várias as causas, tema aliás que vem sendo tratado na relação com os recursos desde Malthus para não ir mais longe.

PS: Caro Leonardo Boff, desde há muito que o leio, creio que vamos no mesmo sentido e se calhar no mesmo barco, complexo por certo, ou real ainda por fazer, fazendo-se. Desde que vi que, antes de mim, você e o Wilson já tinham usado o termo biofilia, que trabalhei aqui [18], que nos senti companheiros.

Li este seu texto [19] enquanto compunha estas palavras que apresento em cima. O meu esforço, nestes últimos tempos, foi fazer pela reabilitação do rigor da Escola Francesa, desgraçadamente banido de cena durante uns tempos pela pérfida orientação da polémica Sokal. Foi agenda política, esta escola de pensamento era a única que se poderia ter oposto à vertigem da adrenalina da aceleração do lucro e do embuste, porque é mais platónica do que aristotélica, vê formas. Agora já está de novo em cima da mesa.

[1] Ivar Ekeland. 1984. Le Calcul, l'Imprevú – les figures du temps de Kepler à Thom. Éditions du Seuil. Paris.

[2] http://www.triplov.com/casquilho/2008/Causticas-de-luz/index.html

[3] http://en.wikipedia.org/wiki/Lyapunov_function

[4] 372.5 singularities] Peirce defines singularity in geometry as (CD 5648): (. . .) An ordinary singularity is one of a set of singularities of which all others are modifications or compounds. Thus, an actual node upon a skew curve is a modification of an apparent node, and ought not to be reckoned as an ordinary singularity. But cusps and inflections, as stationary points and tangents, are ordinary singularities. A higher singularity is one which differs indefinitely little from an aggregation of ordinary singularities.

[5] Alexander Woodcock e Monte Davis. 1984. Théorie des catastrophes. Editions l'Age d' Homme, Lausanne

[6] René Thom (s/ data). Morphogenèse et Imaginaire. Circé 8-9 Cahiers de Recherche sur l' Imaginaire. Pp : 7-24

[7] Jean Petitot-Cocorda. 1992. Physique du Sens – De la  théorie des singularités aux structures sémio-narratives. CNRS, Paris

[8] Petitot. 1985. Local/global in Enciclopédia Einaudi: vol 4, Local/global

[9] René Thom. 1980. Modèles Mathématiques de la Morphogenèse. Christian Bourguois Ed., Paris

[10] 373.2 cusp] A cusp is defined by Peirce as (CD 1412): "a stationary point on a curve where a point describing the curve has its motion precisely reversed" (p. 1412).

[11] cf. Elizabeth Walter-Bense. 2000. Teoria Geral dos Signos. Editora Perspectiva, São Paulo

[12] Jean Petitot. 1983. Théorie des catastrophes et structures sémio-narratives in Sémiotique et théorie des catastrophes. Actes Semiotiques, V, 47-48

[13] Jean Petitot-Cocorda. 1992. Physique du Sens – De la  théorie des singularités aux structures sémio-narratives. CNRS, Paris

[14] Alan Turing. 1952. 'The chemical basis of morphogenesis' from Philosophical Transactions of the Royal Society of London, Series B, No.641, Vol. 237.

[15] G Nicolis. 1995. Introduction to nonlinear science. Cambridge University Press

[16] Affonso G Gomes e Maria Cristina Varriale. 2001.  Modelagem de Ecossistemas: uma introdução. Editora da Universidade Federal de Santa Maria, Santa Maria

[17] Ricard V Solé e Jordi Bascompte. 2006. Self-Organization in Complex Ecosystems. Monographs in Population Biology 42, Princeton University Press

[18] http://www.triplov.com/creatio/casquilho.html

[19] http://www.triplov.com/boff/2009/suicidario.htm