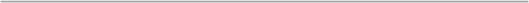envelope da elipse

Caustica é o nome de uma curva, ou superfície, definida como o envelope dos raios de luz reflectidos, ou refractados, por uma dada curva, a partir de um foco radiante, emissor. Em matemática, um envelope de uma família de variedades é uma variedade que é tangente a cada membro da família em algum ponto. Banchoff (1990) mostra que os raios emergindo dos pontos focais de uma elipse formam uma caustica, e, acrescentando mais uma dimensão constrói a superfície de catástrofe da aplicação normal, o desdobramento espacial do envelope.

superfície de catástrofe da elipse (Banchoff)

O conceito matemático de envelope como variedade, vem da abstracção de fenómenos ópticos, pois a palavra caústica vem do termo grego καυστός que significa queimar, através do latim causticos, e aplica-se na descrição de imagens formadas pela luz, quando atravessa um vidro ou água.

cáustica de luz

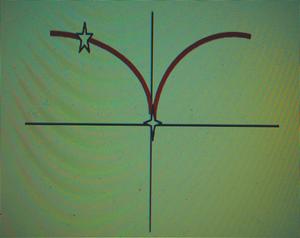
Nas causticas aparecem pontos de cúspide de que o diagrama seguinte dá uma ilustração. Peirce deu uma interpretação cinemática definindo o ponto de cúspide como sendo o sítio estacionário numa curva onde um ponto que se desloca vê o seu movimento invertido.  De acordo com a terminologia de Peirce o gráfico seguinte pode interpretar-se como um sinsigno icónico-remático pela sua natureza de diagrama mas também legisigno icónico-remático porque comporta uma lei.

diagrama do ponto de cúspide através do movimento da estrela

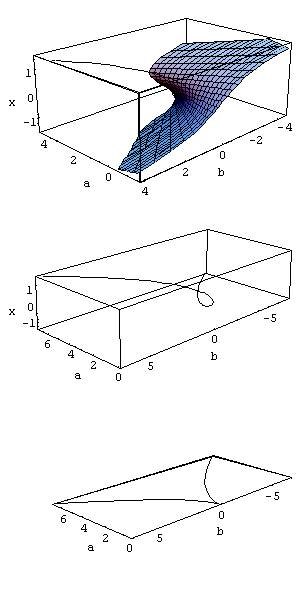
Essa interpretação cinemática não é a única, um ponto de cúspide também pode ser obtido como projecção da curva de contorno da superfície de Riemann-Hugoniot, mais geralmente conhecida como a catástrofe da ruga, que se exemplifica na sucessão de gráficos da figura abaixo. Neste contexto a cúspide adquire o género feminino, passa a ser a designação da curva associada ao ponto, no âmbito da teoria das Catástrofes de René Thom. Neste quadro existe uma função potencial que governa un sistema que se expressa numa dinâmica de gradiente e os pontos onde o gradiente se anula são os equilíbrios, que podem ser estáveis ou instáveis, sendo estes últimos lugares de transição arrumando-se todos numa variedade de equilíbrios.

cúspide obtida como projecção da curva de contorno da ruga

A lei que lhe sucede, dentro da lista de catástrofes elementares elaborada por Thom, designa-se por cauda de andorinha. É a figura da deixis (Petitot, 1983) e inspirou o último quadro de Dali. Arnold (1986) refere que no espaço 3-Dimensional as únicas singularidades estáveis dentro do conceito de causticas são a cúspide e a cauda de andorinha, todas as outras dissolvendo-se perante pequenas perturbações. Se a cuspide permite a esquematização da crise (Mourão e Casquilho, 2000), que possa a cauda de andorinha anunciar novos tempos.

cauda de andorinha (Banchoff)

Referências

Adriano D. Rodrigues. 1996. Dimensões Pragmáticas do Sentido. Edições Cosmos, Lisboa.

Elizabeth Walther-Bense. 2000. A Teoria Geral dos Signos. Editora Perspectiva. São Paulo.

Jean Petitot. 1983. Théorie des catastrophes et structures sémio-narratives in Sémiotique et théorie des catastrophes. Actes Semiotiques, V, 47-48

José Augusto Mourão e José Casquilho. 2000. Catástrofes fiduciárias: o valor ondulatório do dinheiro. Comunicação e Sociedade, Cadernos do Noroeste, vol 14 (1-2), 193-204.

Michel Demazure. 1989. Catastrophes et Bifurcations. Éditions Ellipses, Paris.

Thomas F. Banchoff. 1990. Beyond the Third Dimension. Scientific American Library. New York.

Vladimir I. Arnold. 1986. Catastrophe Theory. Springer-Verlag, New York.